
Grifters, Skeptics, and Marks
We’re in the golden age of grift. Where adventurers once flocked to California and the Yukon because “there was gold in them thar hills,” the best way to get rich these days is to fleece suckers. We’ve got crypto rug pulls, meme stocks, CAT bonds for retail investors; meanwhile, the regulatory landscape is becoming increasingly lax, with financial professionals frequently joking, “crime is legal now.”
TODO: youtube citation for crime and CAT bonds
Now, this is hardly the first time in history this has happend. The Great Depression brought with it a wave of con artists, as portrayed in movies like Paper Moon or The Sting. A century earlier, Mark Twain wrote of the innumerable swindlers and card sharps of his day; he lost most of his own fortune investing in doomed investment schemes When the conditions are right, they seem to crawl out of the woodwork.
For example, this WWI era comic is still perfectly relevant today, with influencers routinely shilling products without declaring affiliation:

The question: is this just the new normal, and things are just going to keep getting worse? Or is there some reason why it comes in waves? If so, is it driven by external circumstances such as war or poverty, or is it a natural fluctuation?
The answer, I’d argue, lies in a moderately obscure mathematical theory from the 1980’s.
Evolutionary Game Theory
John Maynard Smith
Evolution and The Theory of Games

Note that triange diagram on the cover of the book; we’ll be revisting that visualization several times.
Source code available in the Jupyter notebook.
GSM Model
| Players | Grifter | Skeptic | Mark |
|---|---|---|---|
| Grifter | -grifter_loss | -grifter_loss | grift_gain |
| Skeptic | -skeptic_cost | mutual_benefit - skeptic_cost | mutual_benefit - skeptic_cost |
| Mark | -mark_loss | mutual_benefit | mutual_benefit |
When a Grifter meets another Grifter or a Skeptic, the scam fails. The Grifter wastes time and effort and incurs a loss. But when a Grifter meets a Mark does the strategy pay off: the Grifter successfully exploits the Mark and gains a sizable reward.
A Skeptic never gets scammed, but pays a constant price for vigilance. When a Skeptic meets anyone—Grifter, Skeptic, or Mark—they incur an constant overhead cost, which represents costs investing in education and doing due diligence. When interacting with honest counterparts (Skeptics or Marks), they still achieve mutual cooperation, but still have to pay the cost for their caution.
A Mark is trusting and unguarded. When a Mark meets another Mark, everything goes smoothly: they cooperate without hesitation and both receive maximal payoffs. Things go almost as well when they meet a Skeptic; after the Skeptic has done their homework the two are able to cooperate without issue, and the Mark still recieves a maximal payoff.
It’s only when a Mark encounters a Grifter that things go south. The Mark is exploited and incurs a large loss.
TODO Here are some reasonable parameter values:
| parameter_name | value | note | |
|---|---|---|---|
| mutual_benefit | 1.0 | mutual benefit of cooperation | |
| skeptic_cost | 0.2 | overhead of being a skeptic | |
| grift_gain | 1.5 | payoff for a Grifter exploiting a Mark | |
| mark_loss | 2.0 | loss suffered by a Mark when exploited | |
| grifter_loss | 0.5 | cost of a failed grift | |
Which results in
| Players | Grifter | Skeptic | Mark |
|---|---|---|---|
| Grifter | -0.5 | -0.5 | 1.5 |
| Skeptic | -0.2 | 0.8 | 0.8 |
| Mark | -2.0 | 1.0 | 1.0 |
Replicator Dynamics
def replicator(populations, A, delta=0.05, N=2000):
"""
Given an initial vector of `populations`, an payoff matrix `A`, a step size
`delta`, and a number of iterations `N`, return the trajectory as a 2D
numpy matrix and the final population as a 1D numpy array the same shape as
the population.
"""
# ensure populations is a normalized numpy vector
populations = np.asarray(populations, float)
populations = populations / populations.sum()
# initialize the trajectory with the initial conditions
trajectory = [populations.copy()]
for _ in range(N):
# payoff for this iteration
fitness = A @ populations
# update population in direction of the most successful strategy
average = populations @ fitness
populations = populations + delta * (populations * (fitness - average))
# avoid extinction and normalize
populations = np.clip(populations, 1e-6, 1 + delta)
populations = populations / populations.sum()
# track the full history of population trajectories
trajectory.append(populations.copy())
return np.array(trajectory), populations
Results
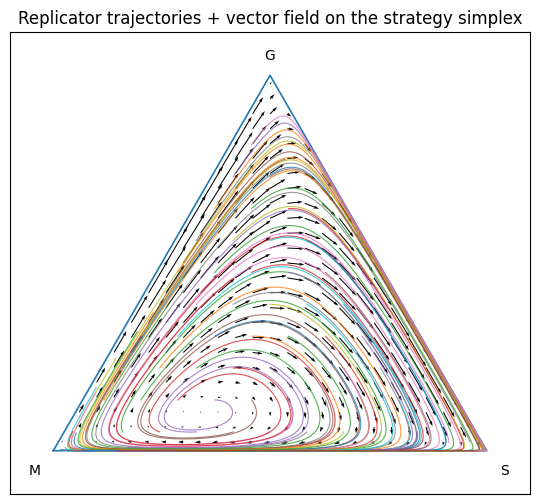
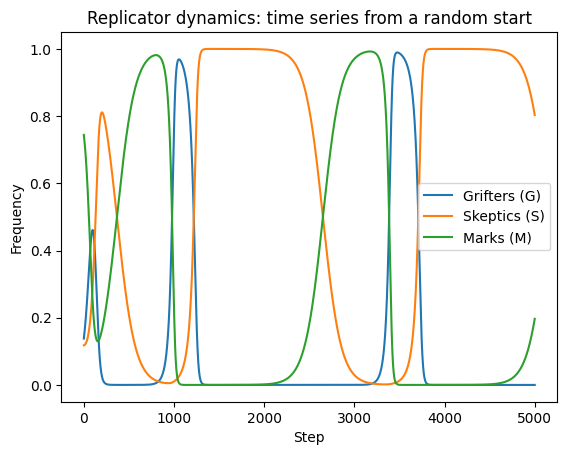
Variations
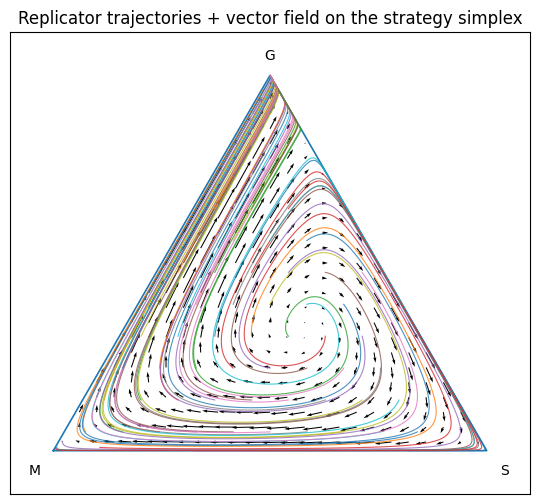
Discusses “asymmetric games with cyclical dynamics.”
Non-transitive games (rock-paper-scissors game where every strategy can be beat by at least one other) always lead to these kinds of cyclical dynamics and do not converge to a single equilibrium point.
Golden Age of Grift, “crime is legal now.”
Evolutionary Game Theory, toy models, qualitative behavior.
Due diligence and education, I’m convinced this is a constant cost.
Non-transitive relationships causes the system to converge not a single point but to an orbit. Not uncommon; many predator/prey ecological models also fall into periodic orbits.
“Lilies of the valley” - Marks have a higher payoff in a high-trust environment with fewer grifters. Trust is efficient and easy, so long as most people are trustworthy.
Paper Moon.
Sensitive to parameters, other scenarios, like the cost of skepticism being too high leads to extinction.
Hawks, Doves, and Retaliators
Compare to Hawks, Doves, and Retaliators, which leads to a fairly boring equilibrium.
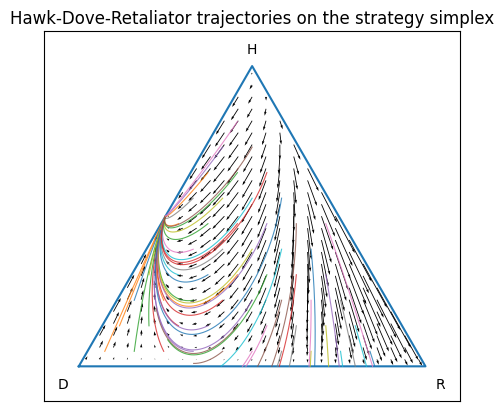
Vigilante justice ultimately doesn’t work. Due diligence does work, but once there are sufficient consumer protections in place that you are exceedingly unlikely to be scammed, everyone lowers their guard (or forgets how to raise it at all) and soon the population is ripe for a new generation of grifters. They do well for a while, until their very success leads to numerous copycats, which leads to a low-trust environment, which brings the skeptics back… there’s no way for the system to every truly stabilize.
Staying as a permanent skeptic has a higher payoff than any other permanent strategy, but fixing a strategy is not optimal. The worst strategy is to do whatever worked a dozen iterations ago, because by then the population mix has evolved to exploit that. The theoretically best strategy is to be aware of the current mix and switch just before its about to change. Note that such advanced, memory based strategies are out-of-scope of this EGT model, and if they were possible we would have to include them as a separate population, which in turn would change the dynamics, on so on ad infinitum. This is why human behavior en masse is so hard to model: there isn’t some “grifter” gene that fixes an individuals behavior for life, but a rational decision based on innumerable factors.
TODO: Which AI lies best?